算法与数据结构

整数

整数除法

题目： 给定两个整数 a 和 b ，求它们的除法的商 a/b ，要求不得使用乘号 '*'、除号 '/' 以及求余符号 '%' 。

注意： 整数除法的结果应当截去（truncate）其小数部分，例如：truncate(8.345) = 8 以及 truncate(-2.7335) = -2 假设我们的环境只能存储 32 位有符号整数，其数值范围是 [−2^31, 2^31−1]。本题中，如果除法结果溢出，则返回 2^31 − 1

const divide = (a, b) => {
  // 当被除数为- 2^31,除数为 -1 时   才会除法溢出
  if (a === -Math.pow(2, 31) && b === -1) { return Math.pow(2, 31) - 1 }

  let p = 0 // 0-正，1-负
  if (a > 0 && b > 0) { p = 0 }
  else if (a < 0 && b < 0) { p = 0 }
  else { p = 1 }

  // 将两个数都变为正数
  if (a < 0) { a = -a }
  if (b < 0) { b = -b }

  let res = 0
  // 用减法来代替除法，如15/2就是循环15减去7个2
  while (a >= b) {
    a -= b
    res++
  }

  return p ? -res : res
}

二进制加法

题目： 给定两个 01 字符串 a 和 b ，请计算它们的和，并以二进制字符串的形式输出。输入为 非空 字符串且只包含数字 1 和 0。

解法一：
/**
 * @param {string} a
 * @param {string} b
 * @return {string}
 */
const addBinary = (a, b) => {
  // 0b 表示二进制，0o表示八进制，0x表示十六进制
  return (BigInt('0b' + a) + BigInt('0b' + b)).toString(2);
}

解法二：
/**
 * @param {string} a
 * @param {string} b
 * @return {string}
 */
const addBinary = (a, b) => {
  // 补齐两个字符串的长度
  const len = Math.max(a.length, b.length)
  if (a.length < len) {
    while (a.length < len) {
      a = '0' + a
    }
  }
  if (b.length < len) {
    while (b.length < len) {
      b = '0' + b
    }
  }
  // 定义一个变量来存储下次运算是否需要+1
  let isPlusOne = 0, ans = ''
  for (let i = len - 1; i >= 0; i--) {
    let tempA = a[i]
    let tempB = b[i]
    let sum = Number(tempA) + Number(tempB) + isPlusOne
    isPlusOne = sum > 1 ? 1 : 0
    ans = sum % 2 + ans 
  }
  if (isPlusOne) { ans = isPlusOne + ans }
  return ans
}

比特位计数

题目： 给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

示例： 输入5，输出[0,1,1,2,1,2]

解法一：
/**
 * @param {number} n
 * @return {number[]}
 */
const countBits = (n) => {
  const bits = [0]
  for (let i = 1; i <= n; i++) {
    bits[i] = i.toString(2).split('').reduce((pre, cur) => {
      return cur === '1' ? parseInt(pre) + 1 : parseInt(pre)
    }, 0)
  }
  return bits
}

解法二：
位运算+动态规划
&    与      两个位都为1时，结果才为1
|    或      两个位都为0时，结果才为0
^    异或    两个位相同为0，相异为1
~    取反    0变1，1变0
<<   左移    各二进位全部左移若干位，高位丢弃，低位补0
const countBits = (n) => {
  const dp = [0]
  for (let i = 1; i <= n; i++) {
    // 1、对于任一数 i，它二进制数中 1 的个数 = i 右移一位 的 1 的个数 + i 末位 1 的个数
    // 2、判断奇偶用且运算：如果 i 是偶数，i & 1 === 0；如果是奇数，i & 1 === 1；
    dp[i] = dp[i >> 1] + (i & 1)
  }
  return dp
}

只出现一次的数字 (opens new window)

题目： 给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。

示例： nums = [2,2,3,2]

/**
 * @param {number[]} nums
 * @return {number}
 */
const singleNumber = function(nums) {
  const map = new Map()
  for (const num of nums) {
    map.set(num, (map.get(num) || 0) + 1)
  }
  for (const [key, val] of map) {
    if (val === 1) {return key}
  }
};

最大单词长度乘积 (opens new window)

题目： 给定一个字符串数组 words，找到 length(word[i]) * length(word[j]) 的最大值，并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词，返回 0。

示例1：

输入: ["abcw","baz","foo","bar","xtfn","abcdef"]
输出: 16 
解释: 这两个单词为 "abcw", "xtfn"。

示例2：

输入: ["a","aa","aaa","aaaa"]
输出: 0 
解释: 不存在这样的两个单词。

// 方法一：
const maxProduct = function(words) {
  const bits = [], len = words.length
  // 预排序，字符串长的排在前面
  words.sort((a, b) => b.length - a.length)
  for (let i = 0; i < words.length; i++) {
    let word = words[i]
    // 生成掩码，出现 a 对应掩码第一位为 1，以此类推
    for (const letter of word) {
      bits[i] |= 1 << (letter.charCodeAt(0) - 97)
    }
  }
  let ans = 0;
  for(let i=0; i<len-1; i++){
    // 如果循环一开始的两字符串乘积小于 ans 则后面不可能出现更大的乘积了
    if(words[i].length * words[i+1].length <= ans) break;
    for(let j=i+1; j<len; j++){
      if(words[i].length * words[j].length <= ans) break;
      // 通过与运算判断来两个字符串是否包含相同字母，与运算为 true 代表具有相同字母，因此这里取非
      if(!(bits[i] & bits[j])) {
        ans = words[i].length * words[j].length;
        break;
      }
    }
  }
  return ans
};


// 方法二:
const maxProduct = (words) => {
  // 构建字符二位数组
  const stringArray = new Array(words.length).fill(0).map(x => new Array(26).fill(0))
  // 记录每个字符在二维数组中的位置
  for (let i = 0; i < words.length; i++) {
    for (const char of words[i]) {
      stringArray[i][char.charCodeAt(0) - 'a'.charCodeAt(0)] = true
    }
  }
  let ans = 0
  // 对words里面的字符串两两比较
  for (let i = 0; i < words.length; i++) {
    for (let j = i + 1; j < words.length; j++) {
      let k = 0 // k单独定义是因为要判断没有重复的情况
      for (; k < 26; k++) {
        if (stringArray[i][k] && stringArray[j][k]) { break }
      }
      // 如果k=26就说明，没有字符是重复的
      if (k === 26) { ans = Math.max(ans, words[i].length * words[j].length) }
    }
  }
  return ans
}

排序数组中两个数字之和

题目： 给定一个已按照 升序排列 的整数数组 numbers ，请你从数组中找出两个数满足相加之和等于目标数 target 。

函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 0 开始计数 ，所以答案数组应当满足 0 <= answer[0] < answer[1] < numbers.length 。

假设数组中存在且只存在一对符合条件的数字，同时一个数字不能使用两次。

示例：

输入：numbers = [1,2,4,6,10], target = 8
输出：[1,3]
解释：2 与 6 之和等于目标数 8 。因此 index1 = 1, index2 = 3

输入：numbers = [2,3,4], target = 6
输出：[0,2]

输入：numbers = [-1,0], target = -1
输出：[0,1]

解法： 双指针

/**
 * @param {number[]} numbers
 * @param {number} target
 * @return {number[]}
 */
const twoSum = (numbers, target) => {
  let [left, right] = [0, numbers.length - 1]
  while (left < right) {
    if (numbers[left] + numbers[right] > target) { right-- }
    else if (numbers[left] + numbers[right] < target) { left++ }
    else {
      return [left, right]
    }
  }
}

数组

三数之和 (opens new window)

题目： 给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。答案中不可以包含重复的三元组。

示例：

示例 1：
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

示例 2：
输入：nums = []
输出：[]

示例 3：
输入：nums = [0]
输出：[]

解法：

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
const threeSum = (nums) => {
  if (nums.length >= 3) {
    nums = nums.sort((a, b) => a - b) // 先对数组排序
    let [len, res] = [nums.length, []]
    for (let i = 0; i < len; i++) {
      if (nums[i] > 0) { break }  // 如果第一个数大于0，那么三个数之和肯定大于0
      if (i > 0 && nums[i] === nums[i - 1]) { continue }  // 去重
      let leftIndex = i + 1, rightIndex = len - 1
      while (leftIndex < rightIndex) {
        const sum = nums[leftIndex] + nums[i] + nums[rightIndex]
        if (sum > 0) {
          rightIndex--
        } else if (sum < 0) {
          leftIndex++
        } else {
          res.push([nums[i], nums[leftIndex], nums[rightIndex]])
          while (leftIndex<rightIndex && nums[leftIndex] === nums[leftIndex + 1]) { leftIndex++ } // 去重
          while (leftIndex<rightIndex && nums[rightIndex] === nums[rightIndex + 1]) { rightIndex++ }  // 去重
          leftIndex++
          rightIndex--
        }
      }
    }
    return res
  } else {
    return []
  }
}

长度最小的子数组 (opens new window)

题目： 给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例：

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

**解法：**滑动窗口

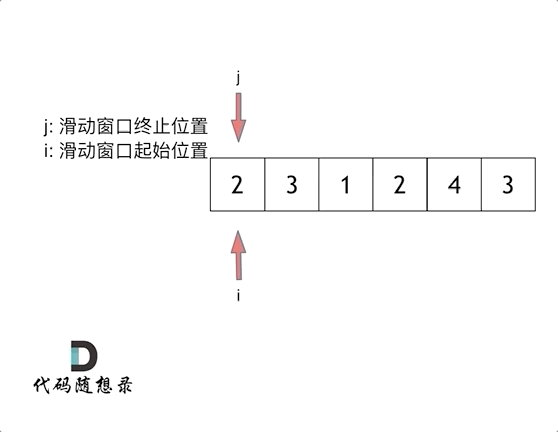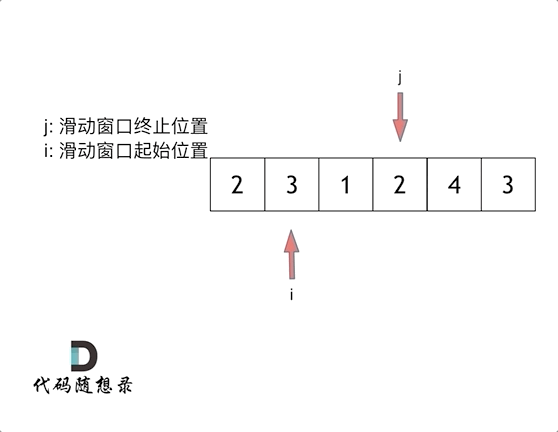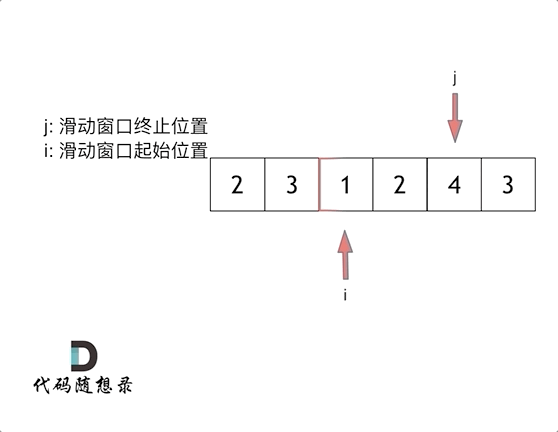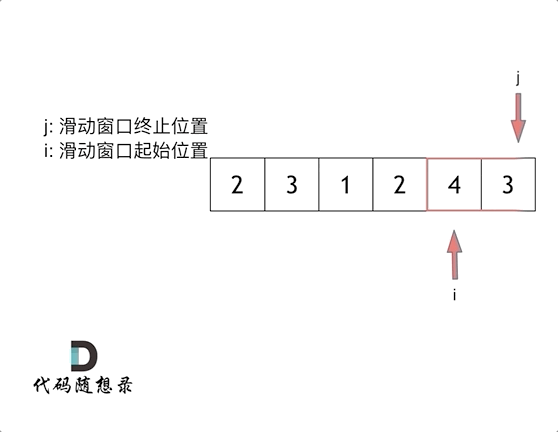
示例：

/**
 * @description 长度最小的子数组
 * @param {number} target
 * @param {number[]} nums
 * @return {number}
 */
const minSubArrayLen = (target, nums) => {
  const len = nums.length
  let [ans, L, R, sum] = [len + 1, 0, 0, 0]
  while (R < len) {
    sum += nums[R]
    while (sum >= target) {
      ans = Math.min(ans, R - L + 1)
      sum -= nums[L]
      L++
    }
    R++
  }
  return ans > len ? 0 : ans
}

乘积小于 K 的子数组 (opens new window)

题目： 给定一个正整数数组 nums和整数 k 。请找出该数组内乘积小于 k 的连续的子数组的个数。

示例：

示例 1:
输入: nums = [10,5,2,6], k = 100
输出: 8
解释: 8个乘积小于100的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于100的子数组。


示例 2:
输入: nums = [1,2,3], k = 0
输出: 0

**解法： ** 滑动窗口

/**
 * @description 乘积小于K的子数组
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
const numSubarrayProductLessThanK = (nums, k) => {
  if (k <= 1) { return 0 }
  const len = nums.length
  let [R, L, ans, accumulate] = [0, 0, 0, 1]
  while (R < len) {
    accumulate *= nums[R]
    while (accumulate >= k) {
      accumulate /= nums[L]
      L++
    }
    ans += R - L + 1
    R++
  }
  return ans
}

和为K的子数组 (opens new window)

**题目：**给定一个整数数组和一个整数 **k，**你需要找到该数组中和为 k 的连续的子数组的个数。

示例：

示例 1:
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。

题解：

const subarraySum = (nums, k) => {
  const mp = new Map();
  mp.set(0, 1);
  let count = 0, pre = 0;
  for (const x of nums) {
    pre += x;
    if (mp.has(pre - k)) { count += mp.get(pre - k) }
    if (mp.has(pre)) { mp.set(pre, mp.get(pre) + 1) }
    else { mp.set(pre, 1) }
  }
  return count;
}

树形结构扁平化

题目：将一个树形的结构转换成数组。

示例：

const tree = [
  {
    name: '小明',
    id: 1,
    pid: 0,
    children: [
      {
        name: '小花',
        id: 11,
        pid: 1,
        children: [
          {
            name: '小华',
            id: 111,
            pid: 11,
          },
          {
            name: '小李',
            id: 112,
            pid: 11,
          }
        ]
      },
      {
        name: '小红',
        id: 12,
        pid: 1,
      }
    ]
  },
  {
    name: '小王',
    id: 2,
    pid: 0,
    children: [
      {
        name: '小林',
        id: 21,
        pid: 2,
      },
      {
        name: '小李',
        id: 22,
        pid: 2,
      }
    ]
  }
]

题解：

// 广度优先遍历
const treeToArray = (tree) => {
  const queue = tree, ans = []
  while (queue.length) {
    const currentNode = queue.shift()
    ans.push({
      name: currentNode.name,
      pid: currentNode.pid,
      id: currentNode.id
    })
    if (currentNode.children) {
      for (const child of currentNode.children) {
        queue.push(child)
      }
    }
  }
  return ans
}

数组转树形结构

// 递归
const arrayToTree = (arr, pid) => {
  let res = []
  arr.forEach(item => {
    if (item.pid === pid) {
      let itemChildren = arrayToTree(arr, item.id)
      if (itemChildren.length) {
        item.children = itemChildren
      }
      res.push(item)
    }
  })
  return res
}

字符串

含有所有字符的最短字符串 (opens new window)

题目： 给定两个字符串 s 和 t 。返回 s 中包含 t 的所有字符的最短子字符串。如果 s 中不存在符合条件的子字符串，则返回空字符串 "" 。如果 s 中存在多个符合条件的子字符串，返回任意一个。

示例：

示例 1：
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC" 
解释：最短子字符串 "BANC" 包含了字符串 t 的所有字符 'A'、'B'、'C'

示例 2：
输入：s = "a", t = "a"
输出："a"

示例 3：
输入：s = "a", t = "aa"
输出：""
解释：t 中两个字符 'a' 均应包含在 s 的子串中，因此没有符合条件的子字符串，返回空字符串。

题解：哈希表+双指针维护滑动窗口

/**
 * @param {string} s
 * @param {string} t
 * @return {string}
 */
const minWindow = function(s, t) {
  let [l, r, ans, m] = [0, 0, '', new Map()]
  for (const k of t) {
    m.set(k, m.has(k) ? m.get(k) + 1 : 1)
  }
  let needType = m.size;
  while (r < s.length) {
    // 获取当前字符
    const c = s[r];
    // 如果是需要匹配的字符
    if (m.has(c)) {
      // 更新字典表中的次数 - 1
      m.set(c, m.get(c) - 1);
      //  如果次数为0，证明这个字符种类在当前窗口已经集齐了，needType - 1
      if (m.get(c) === 0) needType -= 1;
    }
    // 当needType为0，证明所有需要匹配的字符都已经在当前滑动窗口中
    while (needType === 0) {
      const c2 = s[l];
      // 记录当前滑动窗口的字符
      let newRes = s.slice(l, r + 1);
      // 当新的窗口中的字符长度小于上次的字符长度时，更新结果
      // !res 是在结果值为空的时候需要更新一下第一次匹配的值
      if (!ans || newRes.length < ans.length) ans = newRes;
      // 如果左指针移动过程中出现，字典中的值证明需要匹配的字符已经脱离了当前窗口
      if (m.has(c2)) {
        // 更新表中需要出现的次数
        m.set(c2, m.get(c2) + 1);
        // 更新needType
        if (m.get(c2) === 1) needType += 1;
      }
      // 移动左指针
      l++;
    }
    // 移动右指针
    r++;
  }
  return ans
}

有效的回文 (opens new window)

题目： 给定一个字符串 s ，验证 s 是否是 回文串 ，只考虑字母和数字字符，可以忽略字母的大小写。本题中，将空字符串定义为有效的 回文串 。

示例 1:
输入: s = "A man, a plan, a canal: Panama"
输出: true
解释："amanaplanacanalpanama" 是回文串

示例 2:
输入: s = "race a car"
输出: false
解释："raceacar" 不是回文串

题解： 正则表达+双指针

/**
 * @param {string} s
 * @return {boolean}
 */
const isPalindrome = (s) => {
s = s.toLocaleUpperCase().match(/[0-9A-Za-z]+/g)
  if (!s) return true
  s = s.join('')
  let l = 0, r = s.length - 1
  while (l < r) {
    if (s[l] !== s[r]) { return false }
    l++
    r--
  }
  return true
}

无重复字符的最长子串

题目：给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

思想：滑动窗口

题解：

const lengthOfLongestSubstring = (s) => {
  let l = 0, maxLength = 0, set = new Set()
  for (let r = 0; r < s.length; r++) {
    if (!set.has(s[r])) {
      set.add(s[r])
      maxLength = Math.max(maxLength, set.size)
    } else {
      while (set.has(s[r])) {
        set.delete(s[l])
        l++
      }
      set.add(s[r])
    }
  }
  return maxLength
}

排序

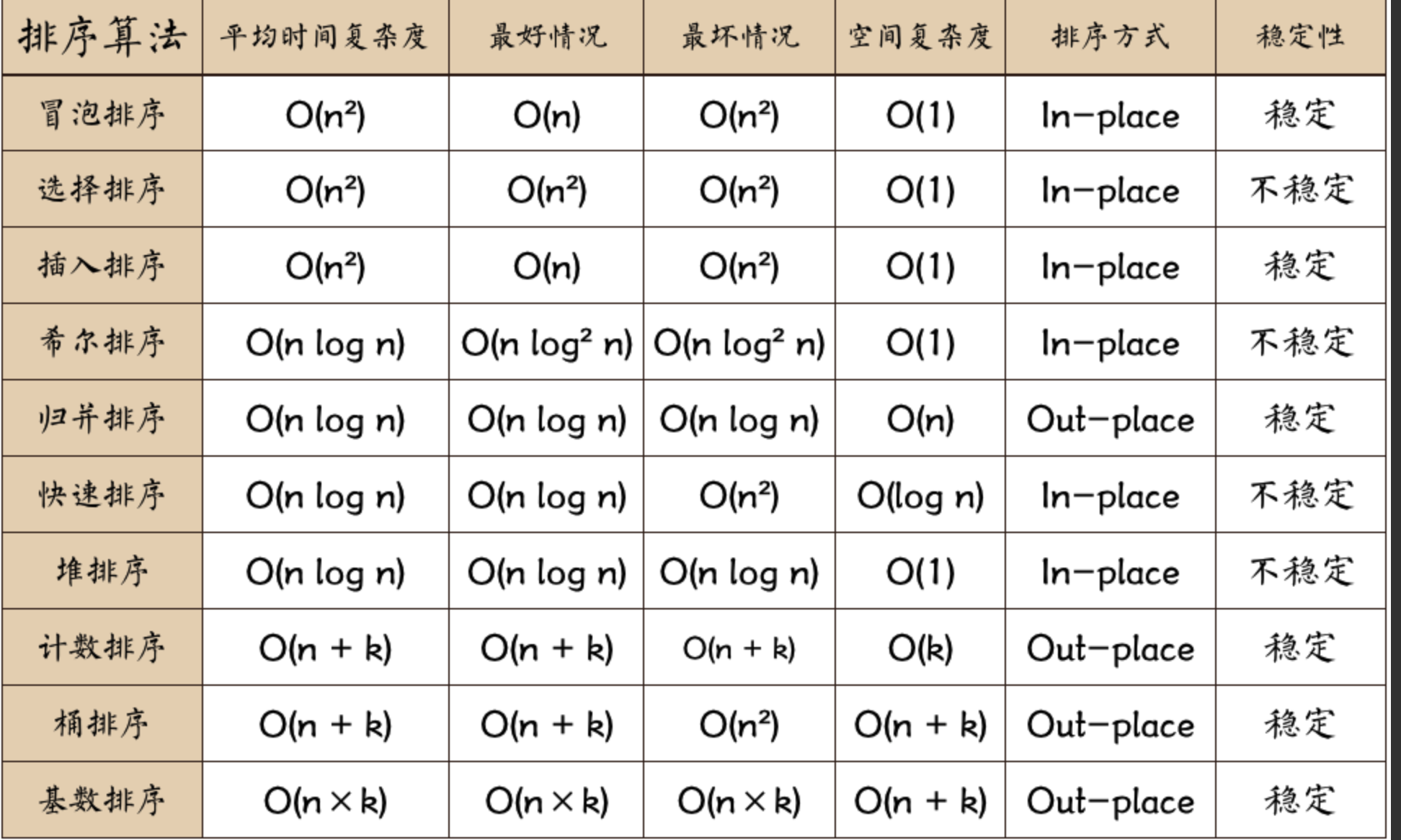
冒泡排序

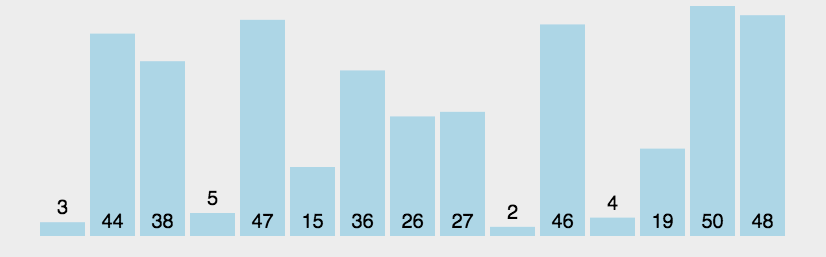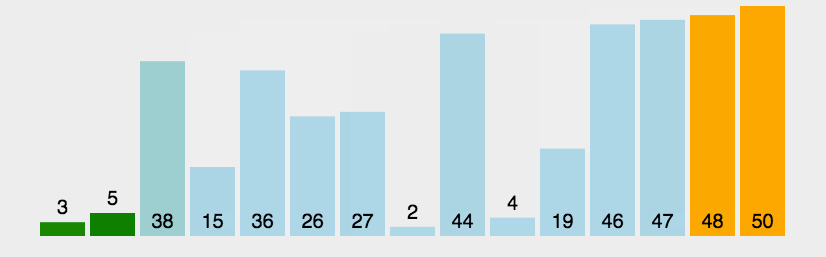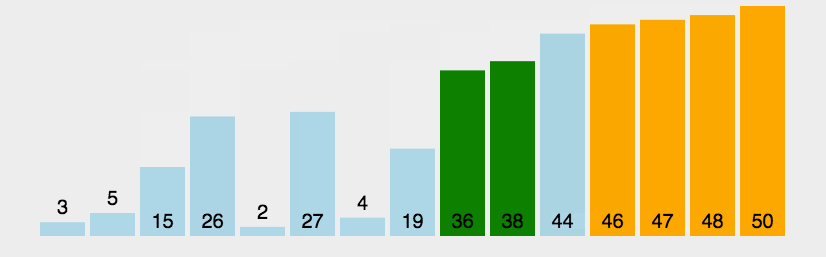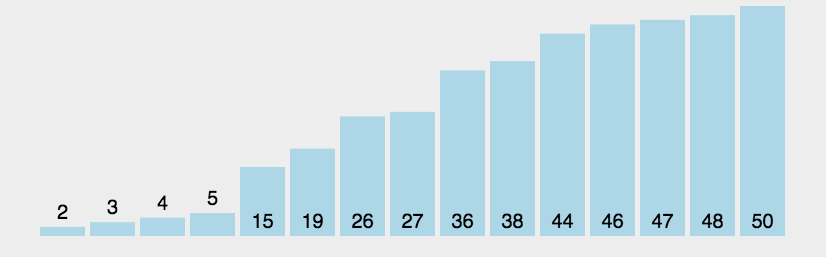
function bubbleSort(arr) {
  let len = arr.length;
  for (let i = 0; i < len; i++) {
    for (let j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j+1]) {        //相邻元素两两对比
        [arr[j],arr[j+1]] = [arr[j+1],arr[j]]  //通过解构完成元素交换
      }
    }
  }
  return arr;
}

let arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(bubbleSort(arr));

选择排序

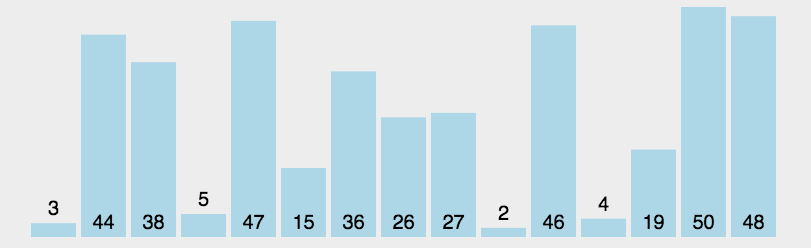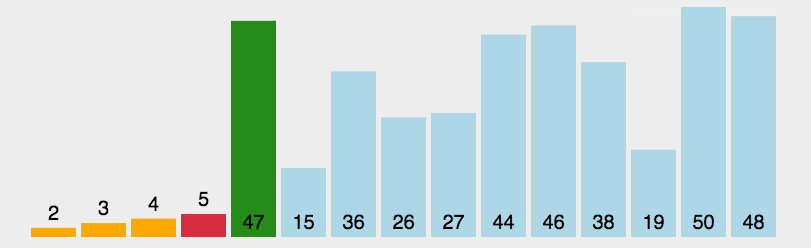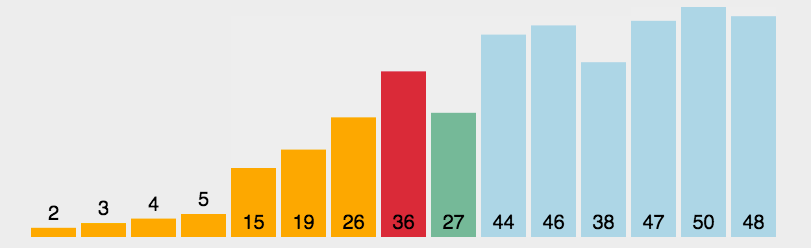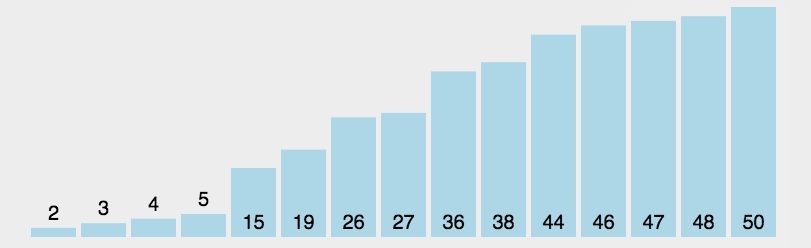
思想：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

function selectionSort(arr) {
  let len = arr.length, minIndex;
  for (let i = 0; i < len - 1; i++) {
    minIndex = i;   //用来保存最小数
    for (let j = i + 1; j < len; j++) {
      if (arr[j] < arr[minIndex]) {     //寻找最小的数
        minIndex = j;                 //将最小数的索引保存
      }
    }
    [arr[minIndex],arr[i]] = [arr[i],arr[minIndex]]  //通过解构完成元素交换
  }
  return arr;
}

let arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(selectionSort(arr));

插入排序

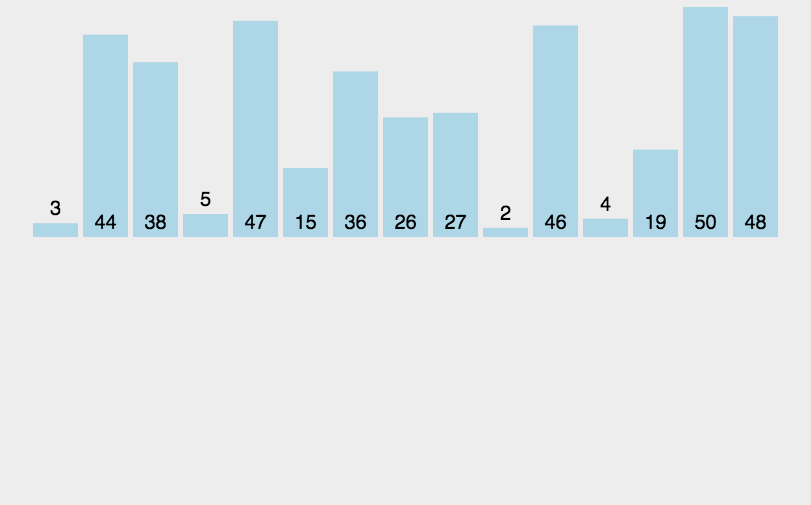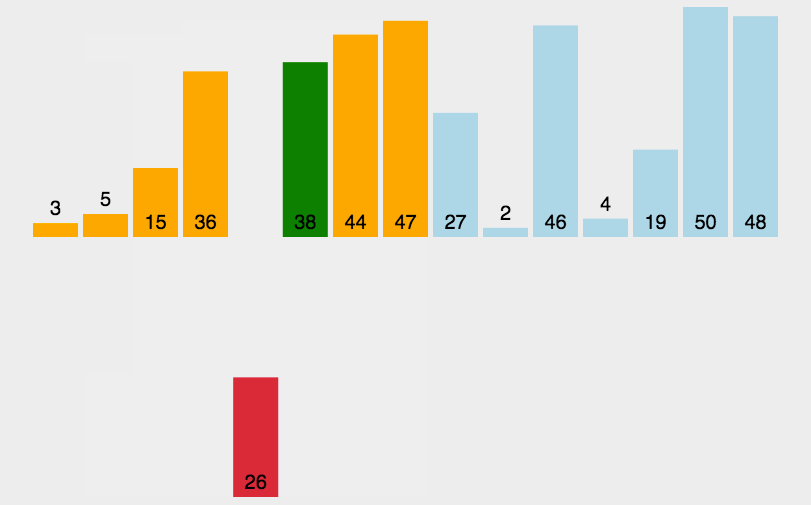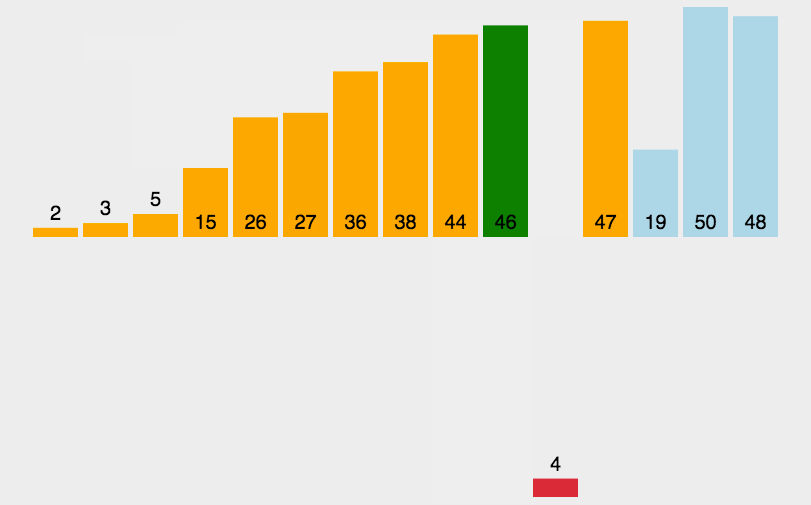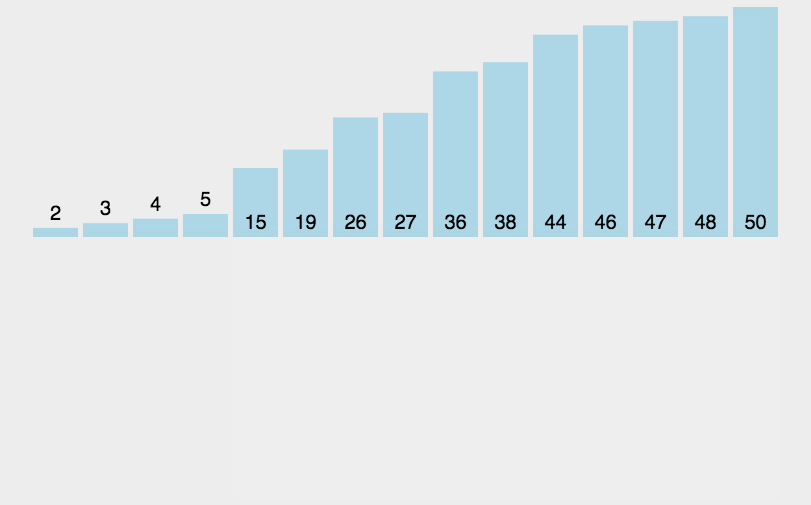
function insertSort(arr) {
  let len = arr.length;
  for(let i = 1; i < len; i++) {  //外循环从1开始，默认arr[0]是有序段
    for(let j = i; j > 0; j--) {  //j = i,表示此时你起在手上的那张牌,将arr[j]依次比较插入有序段中
      if(arr[j] < arr[j-1]) {
        [arr[j],arr[j-1]] = [arr[j-1],arr[j]];  //其实这里内循环中,只要比它前一个数小就交换,直到没有更小的,就break退出.这和动图表示的插入还是有点区别的,但最后结果其实是一样的.
      }
    }
  }
  return arr;
}

let arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(insertSort(arr));

快速排序

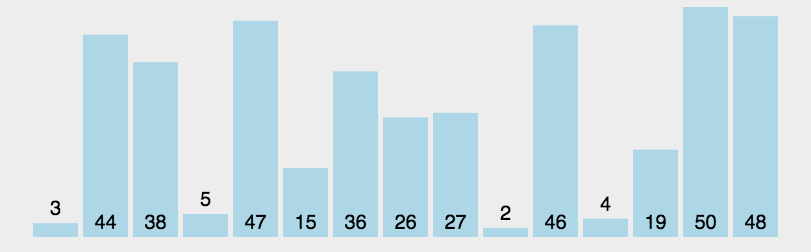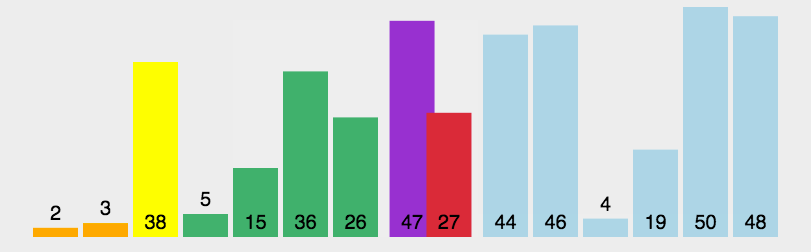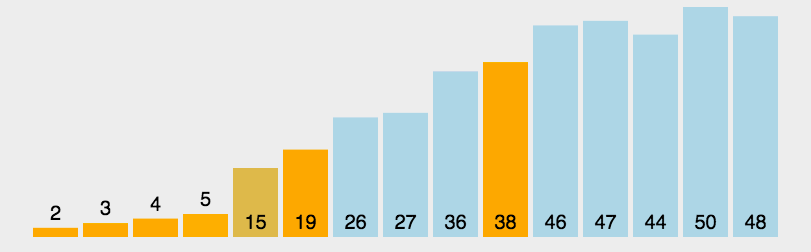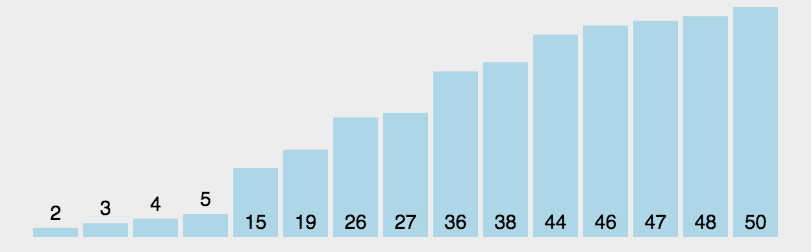
思路：找到一个数作为参考，比这个数字大的放在数字右边，比它小的放在左边； 然后分别再对左边和右变的序列做相同的操作(递归)。快排是冒泡排序基础上的递归分治法。

function quickSort (arr) {
  let len = arr.length;
  if (len <= 1) {
    return arr;
  }
  let left = [], right = [], pivot = arr[0];
  for (let i = 1; i < len; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat(pivot, quickSort(right));
}

let arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(quickSort(arr));

归并排序

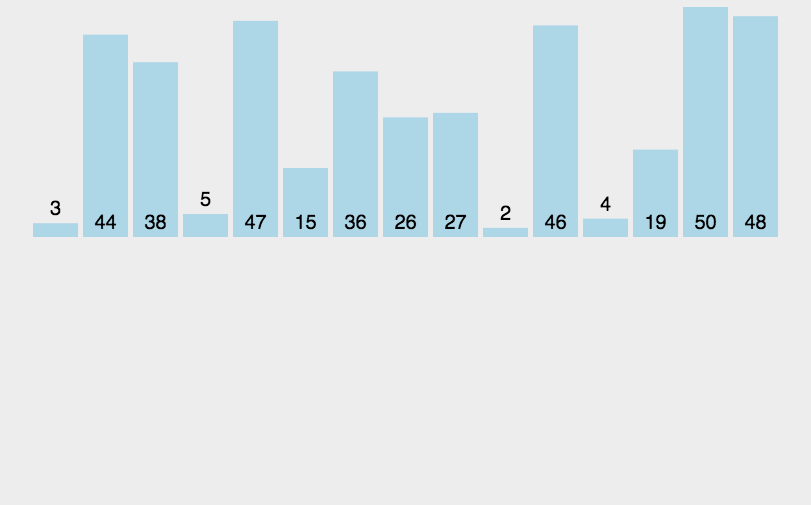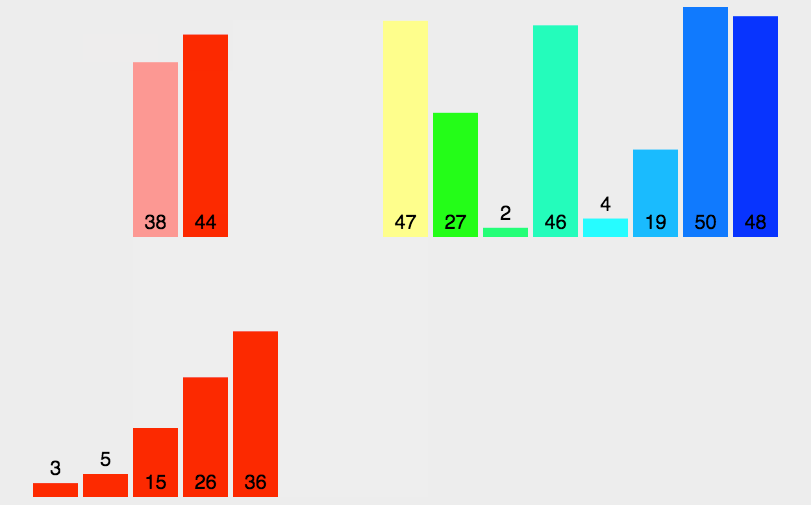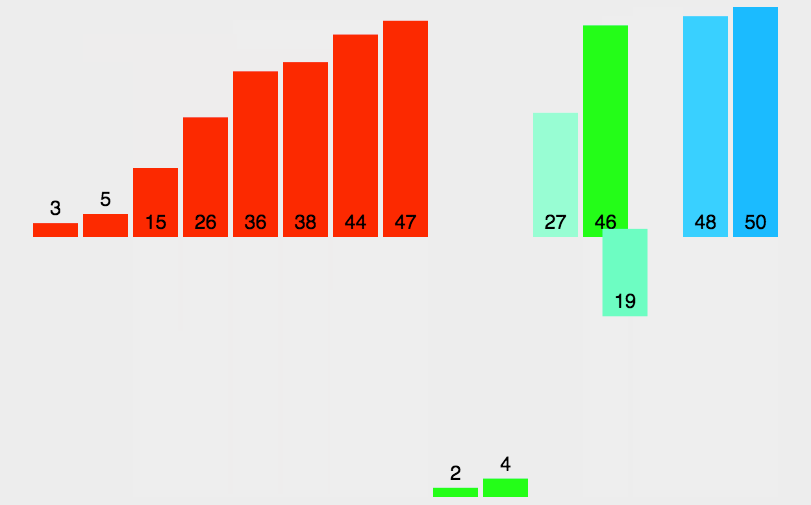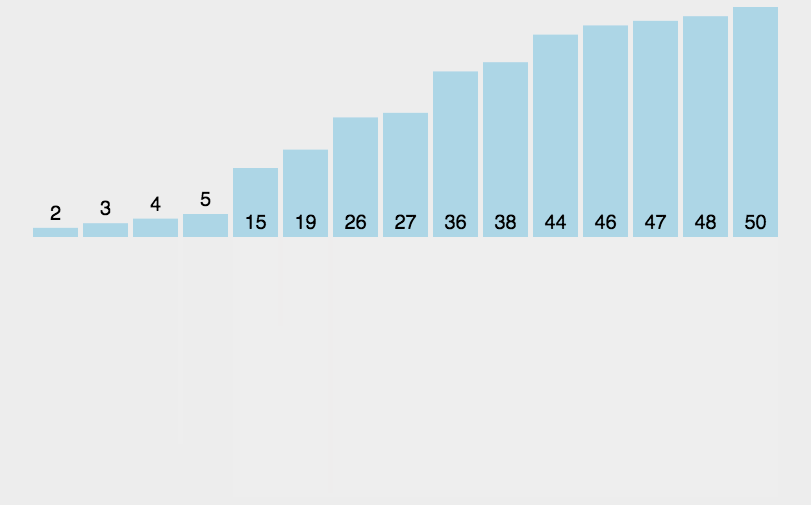
**原理：**归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

function mergeSort(arr) {
  let len = arr.length;
  // 递归出口
  if (len<=1) return arr;
  // 将数组分成左右2份
  let middle = Math.floor(len / 2);
  let left = arr.slice(0, middle), right = arr.slice(middle);
  // 排序递归
  return merge(mergeSort(left), mergeSort(right));
  // 排序函数
  function merge(left, right) {
    let res = [];
    // 左右两边比较
    while (left.length && right.length) {
      if (left[0] <= right[0]) res.push(left.shift());
      else res.push(right.shift());
    }
    // 因为左右两边的数目不一定相等，所以跳出上面的递归之后有可能还有的没有排完
    while (left.length) res.push(left.shift());
    while (right.length) res.push(right.shift());
    return res;
  }
}